The concept of expected value in poker can be best explained with the coin-flipping game. So, let’s play a game. If I flip a coin, and it lands on heads, you will win $5. And, if the coin lands on tails, you will pay me $2.
Heads = +$5
Tails = -$2
If I flip the coin twice, we can have the following outcomes:
Outcome 1 – Win + Win: If the coin lands on the heads twice, you will win $10 from me.
Outcome 2 – Win + Lose: If the coin lands on both heads and tails, you will still win $3 from me.
Outcome 3 – Lose + Lose: If the coin lands on the tails twice, you will lose $4.
As you can guess, this game looks profitable for you in just two flips. But what will happen if I flip the coin over a million times? Will it still be profitable? How much money will you win on an average? To answer these questions, we need to calculate the expected value (EV).
We need to use a formula, which might look scary at first, but it is quite simple to use:
EV = (%W X $W) – (%L X $L)
%W = How often you will win the game? Or, what is your winning percentage?
%L = How often you will lose the game? Or, what is your losing percentage?
$W = How much are you winning?
$L = How much are you losing?
In the above coin-flipping game, we have the following numbers:
%W = How often you will win the game? You have a 50% chance of the coin landing on heads.
%L = How often you will lose the game? Again, you have a 50% chance of the coin landing on tails.
$W = How much are you winning? You are winning $5.
$L = How much are you losing? You are losing $2.
So, let’s calculate the EV:
%W = 0.5 (convert the percentage – 50/100)
%L = 0.5 (convert the percentage – 50/100)
$W = 5
$L = 2
EV = (%W X $W) – (%L X $L)
= (0.5 X 5) – (0.5 X 2)
= 2.5 – 1
= 1.5
So, you have an expected value of $1.5, which means that you will be winning $1.5 in the long run if you play this coin flipping game with me.
What is Expected Value in Poker?
Expected Value (EV) is the average sum of money you can expect to win or lose after making a certain decision. It is the money you are expected to win or lose in the long run when your decision is played over a million times.
You will have either a positive or a negative expected value in poker:
Positive Expected Value (+EV): If you have +EV, you are likely to win money in the long run.
Negative Expected Value (-EV): If you have -EV, you are likely to lose money in the long run.
How to Calculate Expected Value in Poker?
The formula to calculate expected value in poker is:
EV = (%W X $W) – (%L X $L)
While playing poker, you need to answer these questions before you work on the formula:
$W = How much money you will win if you win the hand?
$L = How much money you will lose if you lose the hand?
%W = What is the percentage of winning the hand?
%L = What is the percentage of losing the hand?
Let’s look at an example to calculate the poker expected value.
You are on the Button holding pocket kings in a $1/$2 6-max game. The UTG goes all-in with $20. Everyone else folds. Let’s calculate our poker expected value before making our decision.
$W = How much money you will win if you win the hand?
= $1 (small blind) + $2 (big blind) + $20 (UTG’s all-in)
= $23
$L = How much money you will lose if you lose the hand?
You need to call $20. So, you will be losing $20 if you lose the hand.
%W = What is the percentage of winning the hand?
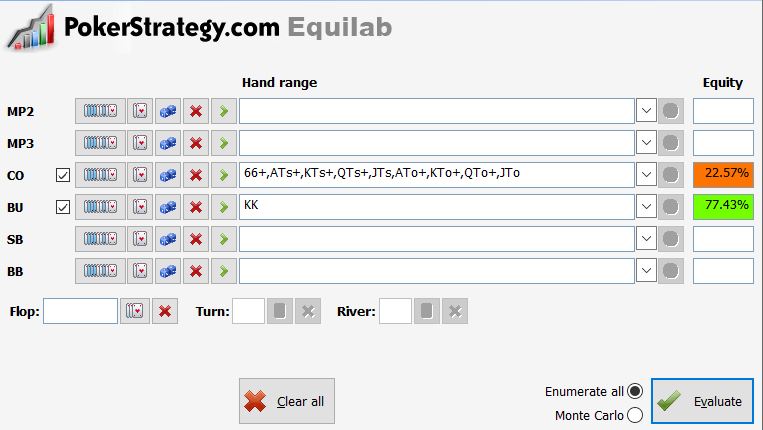
You need to calculate the equity in your hand. You know that your opponent is a tight player who raises with strong hands. If he goes all-in, he must be holding a broadway hand or a pair of sixes and above. If you use an equity calculator like Equilab, you will see that your pocket kings have 77.43% equity. Click here to know more about equity: How to Use Equity in Poker?
%L = What is the percentage of losing the hand?
If you know the equity, then subtract the equity from 100 to get the loss percentage. For example, if your pocket kings have 77.43% equity, then your loss percentage is 22.57% (100 – 77.43). Equilab and other equity calculators usually show this number.
So, we have our numbers ready!
$W = 23
$L = 20
%W = 0.77 (convert the percentage – 77.43/100)
%L = 0.23 (convert the percentage – 22.5/100)
EV = (%W X $W) – (%L X $L)
= (0.77 X 23) – (0.23 X 20)
= 17.71 – 4.6
= 13.11
You have a +EV of $13.11; so, calling here will be profitable in the long run.
NOTE: This does not mean that if you play this hand three times in a row, you will be winning all the three times. Remember, expected value in poker shows you how much you will win or lose on an average if this hand is played over a million times (in the long run).
Why Should You Use Expected Value in Poker?
Always remember that poker is a long-term game, and when you are playing such a game, you should always aim to win money in the long run. So, your goal should be winning money or expecting profit in the long run. When you use the concept of expected value in poker, you will have a clear picture of how much money you are likely to win or lose. Always play when you have a positive expected value, which will yield long-term profits.
As it is quite impossible to calculate EV during live games, you should use it for post-game analysis. You can also create an excel sheet and feed the formula to calculate EV instantly. Create a tab next to your online table and feed the equity, winning and losing amount to calculate the EV. Also, you can try online calculators like RedChipPoker’s Expected Value Calculator to find whether you have a positive or negative EV.
How to Use Expected Value in Poker?
Expected value helps you to make informed decisions in poker. If you know the expected value before calling or raising, you will be a step ahead in the game. Let’s look at the common scenarios where the expected value is useful.
Using Expected Value on a Drawing Hand
The most common dilemma is to decide whether to call a bet on a drawing hand. You haven’t made your hand, but you have outs that can help you win the pot. What to do in such situations? If you analyze your expected value in poker and find out that you have a +EV, calling would be profitable. And, if you see that you have a -EV, you should fold. Let’s look at a raw example where you are not your opponent’s range in any equity calculator:
Your Hand: 5♦ 6♦
Turn: 8♦ K♣ 2♦ 10♠
The pot is $200, and your opponent goes all-in with $100. This is a very typical situation where you have 9 outs, and 1 card is yet to come on the river. What should you do here? Before you make any decision, let’s calculate to see if you have a positive or negative EV.
$W = How much money you will win if you win the hand?
You will be winning the pot of $300 ($200 in the pot + $100 opponent’s all-in) if you win the hand.
$L = How much money you will lose if you lose the hand?
You will be losing $100 (call amount) if you lose the hand.
%W = What is the percentage of winning the hand?
As you have 9 outs, your card odds are 4.1:1 or close to 20% equity.
Click here if you want to know how to calculate card odds: How to Calculate Card Odds and Pot Odds?
%L = What is the percentage of losing the hand?
If your winning percentage is 20, then the loss percentage is 80. (100 – 20 = 80)
Let’s get all the numbers together!
$W = 300
$L = 100
%W = 0.2 (convert the percentage – 20/100)
%L = 0.8 (convert the percentage – 80/100)
EV = (%W X $W) – (%L X $L)
= (0.2 X 300) – (0.8 X 100)
= 60 – 80
= -20
We have a negative EV here of -$20. We will be losing $20 on average if we keep calling for a chance to hit the flush in the long run. So, we should fold here.
Advanced Strategy – Finding the EV of All-in Shove
This might get a little complicated! We will explain each step one by one; so, have a little patience, and you will surely understand this concept.
When you go all-in, there can be only two outcomes:
Outcome 1: Your opponent folds
Outcome 2: Your opponent calls
We will have to evaluate the expected values of both the outcomes to find the overall EV of your all-in shove.
Let’s look at an example: You are on the button with a stack of $100 in a $1/$2 6-max game. A tight-aggressive player from under the gun opens to $10.
Your Hand: 8♠ 9♠
You decide to call, and everyone else folds.
The pot is now $23 ($1 small blind + $2 big blind + $10 bet + $10 call).
Flop: 2♠ 10♦ 4♠
Your opponent c-bets $15. You know that your opponent is a tight-aggressive player who raises from under the gun with broadway hands or a pair of sixes and above. He might be holding a Ten pair or an Ace high. You have a flush draw with 9 outs and decide to call.
The pot is now $53. ($23 already in the pot + $15 bet + $15 call)
Turn: 2♠ 10♦ 4♠ 6♣
This time, your opponent bets $25. The pot is now $78 ($53 already in the pot + $25 bet)
Here, you have a flush draw and an inside straight draw, which makes a total of 12 outs. You can call here but what if you go all-in? What will be the poker expected value of your all-in shove of $75?
But first, we need to find the EV of both the outcomes, as they are a part of your all-in shove.
EV of Outcome 1: Your Opponent Folds
When it comes to folding, you need to know your opponent well. You need to assume the chances (probability) of your opponent folding his hand when you go all-in. In this example, you are assuming that your opponent is most likely to fold 60% of the time when he faces an all-in shove.
W% = If your opponent folds 60% of the time, 60% is your winning chance.
W$ = You win the pot of $78
%L = Zero. There is no loss percentage as your opponent has already folded in this outcome.
$L = Zero. You are not losing any money as your opponent has already folded in this outcome.
EV of Outcome 1 = %W X $W
= 0.6 X 78
= 46.8
So, you are expected to win $46.8 on an average if your opponent folds 60% of the time when you go all-in.
EV of Outcome 2: Your Opponent Calls
In this outcome, your opponent calls your all-in shove of $75. You need to calculate the expected value in poker. So, let’s get our numbers ready.
$W = How much money you will win if you win the hand?
You will be winning $153 ($78 already in the pot + $75 Opponent’s call)
$L = How much money you will lose if you lose the hand?
As you have shoved, you will be losing your remaining $75 at that point of the game.
%W = What is the percentage of winning the hand?
As you have 12 outs, your card odds are 2.8:1 or close to 26% equity.
%L = What is the percentage of losing the hand?
If our winning percentage is 26, then the loss percentage is 74. (100 – 26 = 74)
Let’s get all the numbers together!
$W = 153
$L = 75
%W = 0.26 (convert the percentage – 26/100)
%L = 0.74 (convert the percentage – 74/100)
EV of Outcome 2 = (%W X $W) – (%L X $L)
= (0.26 X 153) – (0.74 X 75)
= 39.78 – 55.5
= -15.72
You have a negative EV of -$15.72. So, you will be losing $15.72 if your opponent calls your all-in shove.
Overall EV of All-in Shove
To calculate the overall EV of your all-in shove, we need to sort out our win/loss percentage and winning/losing amounts for the formula.
%W = What is the percentage of winning?
We are winning only when your opponent folds. So, the fold percentage is our winning percentage.
%W = 60%
$W = How much money you will win?
You are winning $46.8 on an average when your opponent folds 60% of the time.
$W = $46.8
%L = What is the percentage of losing?
You are losing when your opponent calls. If the fold percentage is 60%, calling percentage is your loss percentage. 100 – 60 = 40
%L = 40%
$L = How much money you will lose?
You are losing $15.72 on an average when your opponent calls your all-in shove.
Let’s get the numbers together!
$W = 46.8
$L = 15.72
%W = 0.6 (convert the percentage – 60/100)
%L = 0.4 (convert the percentage – 40/100)
EV of All-in Shove = (%W X $W) – (%L X $L)
= (0.6 X 46.8) – (0.4 X 15.72)
= 28.08 – 6.29
= 21.79
WOW! You have a positive EV of $21.79. This means that your all-in shove under these conditions will be profitable in the long run.
Phew, that was a big one! We know that you must be exhausted with the all-in shove EV. However, the main purpose of going through this onerous calculation is to show how expected value in poker can help make profitable decisions in the long run. Do consider your hand equity and your opponent’s folding percentage as they play an important role in all-in shove.
Conclusion
Expected value in poker does not guarantee any winning or losing amount. It is an expected amount that you are likely to win or lose in the long run. These calculations prove that poker is a game of skill where math can help you to make the right decisions. However, you can’t deny the fact that there is an element of luck involved. The best you can do to deal with luck is to make +EV plays where you will be winning in the long run. So, always calculate your EV before making any decision so that you keep churning out profit for a long time!